David A. Kenny
September 7, 2011
Multiple Groups
Basic Question and Data
Requirement
Does my causal model differ for different groups of persons? Groups must be
categorical and membership must be known. Ideally there should be 200 persons in
each group. If group membership is a latent variable, then we have latent class
or mixture analysis. Note too that group membership should be independent
and so if we have heterosexual married couples we cannot treat husbands and
wives as independent groups.
Data Preparation
Normally, the raw data are inputted. If the covariance matrix is to read,
usually it is computationally more efficient to input the correlation matrix with
the set of standard deviations and means. It is almost always wrong to
estimate a multiple group model analyzing the correlation matrices because
groups usually differ in their variances.
Configural Model
Before beginning to estimate invariance models, it must be established that a
model without any invariances (i.e., the same model in all groups, but
parameters may vary) is a reasonable model. This model is called the configural
model. The fit of this model equals the sum of the chi squares and the
sum degrees of freedom across groups and that fit reveals the extent to which
the underlying structure fits the data when no constraints across groups are
added. Before we can decide that parameter estimates are the same, it
must be established that the configural model is reasonable because all other
models place constraints on that model. Once this is done, then that
model can be used as a basis for comparison to test for invariance. In
comparing models, one often should use a measure of fit like the Tucker-Lewis
Index or RMSEA index and not the chi square difference.
To identify latent means and intercepts, each marker variables intercept is fixed to zero.
Ideally, one searches for the common model using both groups. It is probably inadvisable to use the entire sample because such a strategy uses a mixture of the groups and would be biased toward using the model that favors the larger of the groups.
Invariance of Factor Loadings
Always the first set of values to test for
invariance is the factor loadings. If the factor loadings are not
invariant, then it makes no sense to test the equality of the paths because the
units of measurement would differ across groups. So if the loadings do
not vary, proceed to the next step.
If the loadings are different, the results may be more interpretable if a different marker variable is chosen. Consider for instance a case with four indicators in two groups, the loadings of 2nd through the 4th indicators are invariant. If the 1st indicator were used as the marker, it would appear that the other three loadings are changing across groups when in fact they are invariant. It can be advisable to change the marker variable to determine which loadings are invariant and which are not. One may find that some of the loadings are invariant and others are not; if one has an excess of indictors, one can drop from the model those loadings that differ. To make any claim of invariance, at least one free loading must be fixed to be the same across groups.
Remaining Tests
The next set of tests can be in almost any order, although tests of covariances should be only done if the variances are invariant (and so are tests of equality of correlations). Note that if the parameters are not invariant, then that test might be moved to the bottom list and redone. This is done, because tests of invariance, presume that the parameters tested above are invariant.
Invariance of Paths
The second set of invariances tested is the
invariance of the causal paths. Again this test should only be executed
if the loadings are invariant.
Invariance of Intercepts
The next set of invariances tested might be the
intercepts of the indicators. Again this test should only be executed if
the loadings are invariant.
Invariance of Error Variances
Regardless what has happened above, it is
meaningful to test whether the error variances are the same in both groups,
i.e., homogeneity of error variances. If the paths vary or if both the
loadings and paths vary, such variation should be allowed for this model.
Invariance of Error
Correlation
If the error variances are invariant, we can
test whether the error covariances are equal. In essence, this tests the
equality of the error correlations.
Invariance of Disturbance
Variances
The next test is whether the disturbance
variances are equal. This test is meaningful only if the loadings are
invariant. Even if the paths or the error variances vary, variation in
the variances can still be allowed. This analysis tests what is essentially the
homogeneity of error variance assumption.
Invariance of Disturbance
Correlations
The next test is whether the factor covariances
are equal. This test is only meaningful if the loadings and the factor
variances are invariant. Given equality of the factor variances,
this test evaluates equality of the factor correlations. Note that if this
model fits, then all the parameters in the groups are equal and the data could
be pooled and group should be ignored.
Invariance of Exogenous Factor
Variances
The next test is whether the factor variances
are equal. This test is meaningful only if the loadings are
invariant. Even if the paths or the error variances vary, variation in
the variance can still be allowed.
Invariance of Exogenous Factor
Correlations
The final test is whether the factor covariances
are equal. This test is only meaningful if the loadings and the factor
variances are invariant. Given equality of the factor variances,
this test evaluates equality of the factor correlations. Note that if this model
fits, then all the parameters in the groups are equal and the data could be
pooled and group should be ignored.
Invariance of Factor
Intercepts and Means
The final set of invariances tested is the
intercepts of the endogenous factors and the means of the exogenous factors.
Model of Complete Invariance
In this model all the above parameters in the
groups are set equal. If this is a good fitting model, the grouping variable
has no effect and a single model treating persons as if they were from one
group can be estimated. There would be complete invariance.
Interpretation
If a parameter set is deemed to vary across
groups, to interpret those differences examine the estimates of a previous
model in which that parameter set varies.
Neff Example
This example is taken from
Neff, J. A. (1985). Race and vulnerability to stress: An examination of differential vulnerability. Journal of Personality and Social Psychology, 49, 481-491.
The same model is estimated for 658 Whites and 171 Blacks. The following variables in the model using Neff's notation:
- Y1 - Total undesirable events
- Y2 - Total change events
- Y3 - Nervous upset symptoms
- Y4 - Depressive symptoms
- Y5 - Psychopathological symptoms
- X1 - Total family income
- X2 - Education
- X3 - Age
There appears to be an error in the standard deviation for education of whites. It is changed to .75.
The measurement model is as follows: The first two variables are indicators of a life change or stress factor. The next three are indicators of a mental health factor. The next two are indicators of socioeconomic status or SES and the last is a single indicator variable of age.
The configural structural model is as follows: Age and SES are exogenous and they each cause the endogenous factors. Stress is assumed to cause mental health. The model is presented in Figure 1 of the paper and below:
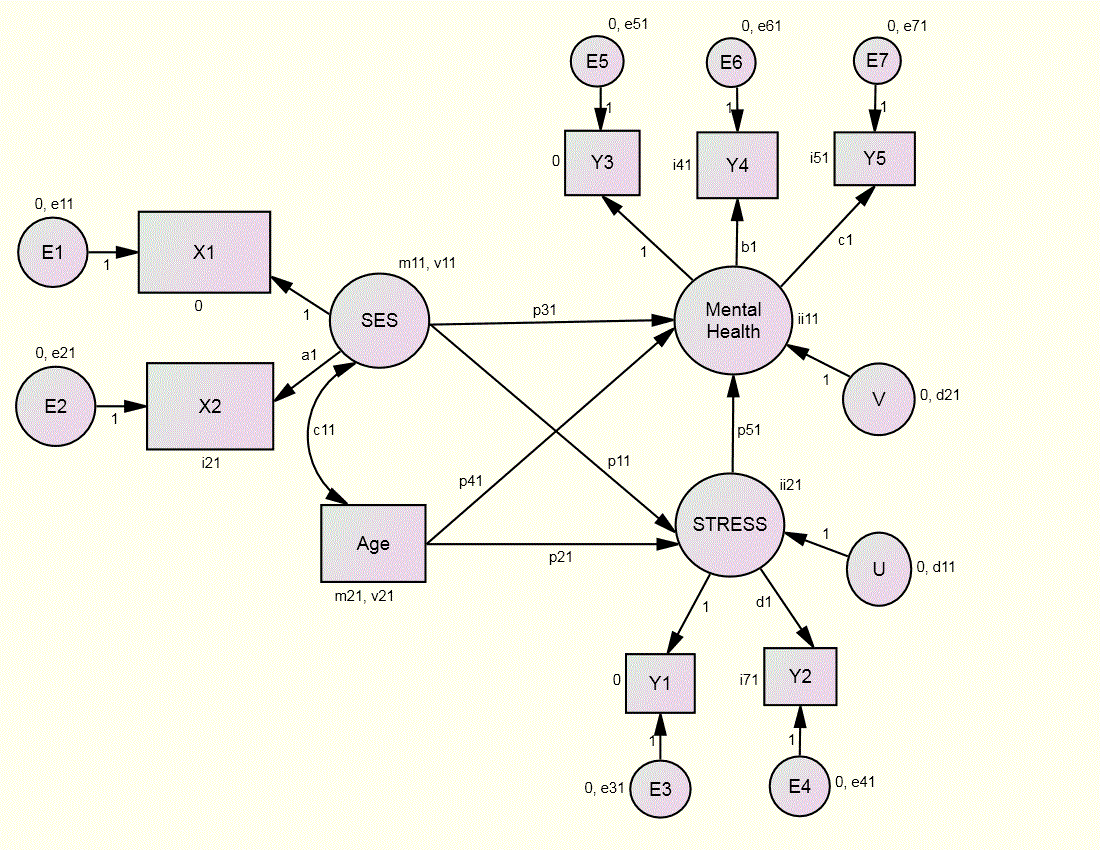
This model has 29 parameters in each group (4 loadings, 5 paths, 4 indicator intercepts, 2 means, 2 latent intercepts, 7 error variances, 2 exogenous variances, 2 disturbance variances, and 1 covariance) and 15 degrees of freedom in each group. The marker variables are Income, Y1, and Y3 and their loadings are set to one and intercepts to zero.
Download the Amos 19 setup and an Excel file with data.
The results from the models described previously are as follows (the model with equal disturbance correlations and equal error correlations are not estimated because they are not contained in the model):
Table 1: Summary of Model Fit with Invariances: A Given Model Has the Constraints of All Models above It
Model |
Chi Square |
df |
p for chi sq. diff. |
TLI |
RMSEA |
Configural |
69.873 |
30 |
---- |
.940 |
.040 |
Equal Loadings |
80.602 |
34 |
.030 |
.938 |
.041 |
Equal Paths |
86.162 |
39 |
.351 |
.945 |
.038 |
Equal Intercepts |
104.963 |
43 |
.001 |
.935 |
.042 |
Equal Disturbance Variances |
122.923 |
45 |
<.001 |
.922 |
.046 |
Equal Exogenous Variances |
126.620 |
47 |
.157 |
.924 |
.045 |
Equal Exogenous Correlation |
132.105 |
48 |
.019 |
.921 |
.046 |
Equal Error Variances |
218.113 |
55 |
<.001 |
.866 |
.060 |
Equal Factor Means and Intercepts |
391.181 |
59 |
<.001 |
.746 |
.083 |
Configural Model: Although the chi square for this model is statistically significant, the RMSEA is acceptable and the TLI is marginal. Thus, the model is a reasonably good fitting model.
Equal Loadings Model: For the Neff study, it appears that the loadings are invariant. Although we see a slight decline in the CFI and a slight increase in the RMSEA, the fit values remain acceptable.
Variable Whites Blacks Summary
X1 1.000 1.000 Education more important for Blacks
X2 0.209
0.491
Y1 1.000 1.000 Total change more important for
Whites
Y2
0.657 0.809
Y3
1.000 1.000 Nervous
more important for Whites
Y4
0.988 1.185
Y5 1.002 1.229
Note that in comparing loadings, their relative size needs to be compared. So if Y4 or Y5 is made the marker the marker, it would be seen more clearly that Y3 is the more variable indicator:
Variable
Whites Blacks
Y3 0.998 0.814
Y4 0.986 0.964
Y5 1.000 1.000
That is, Y3 is considerably lower for Blacks than for Whites.
Equal Paths
Very often the equality of the paths is of central interest. We see that the fit does not worsen when the paths are set equal.
Cause Effect Whites Blacks Summary
SES Stress 0.057
-0.009
SES affects Stress more for Whites
SES Mental-Health -0.081 -0.097
Age Stress 0.004
0.006
Age Mental-Health -0.009 -0.007
Stress Mental-Health 0.127
0.195 Blacks' MH more affected by Stress
They can be tested individually by two different ways. First, and perhaps the easiest but somewhat rough, is to examine the modification indices from the model with equal paths. The square root of a modification index can be treated as an approximate Z test which evaluates making that one path the only one to be unequal across groups. This test, denoted as Z1 below, can be too liberal. Better is to use the equal loading model, and fix one path at a time to be equal across groups and use the chi square difference test to evaluate the model: The fit of this model is compared to the model with all paths equal. Again the square root of chi square, denoted as Z2 below, evaluates the equality of loadings. We see below that there are no race differences in any of the paths:
Cause Effect
Z1 Z2
SES Stress 1.78 0.72
SES Mental Health 1.19 0.24
Age Stress
-1.52 -0.30
Age Mental Health -1.30 -0.36
Stress Mental Health -1.22 -0.90
*White path minus the Black path
There is a marginally significant difference that higher SES causes greater Stress more strongly for Whites than Blacks, but this uses the liberal modification test.
Equal Intercepts
The non-zero marker variables are allowed to have different intercepts.
Variable Whites Blacks
Summary
X1
0.000
0.000 Whites
have relatively more income and less education than Blacks.
X2
0.570 0.693
Y1
0.000
0.000 Whites
score relatively higher on Y1 and lower on Y2 than
Blacks.
Y2 -0.177
-0.045
Y3
0.000
0.000 Blacks
score relatively higher on Y4 than Whites.
Y4
0.006 0.185
Y5 -0.012
0.054
We note that the fit worsens some imposing these constraints. Likely most of that decline is due to Y4 and if that indicator were dropped the fit decline might disappear.
Equal Disturbance Variances
We force the two disturbance variances to be equal across Whites and Blacks. Variance due to the exogenous variables is removed.
Variable Whites
Blacks
Summary
Stress
0.735 0.444 Whites more
variable
Mental-Health 0.077
0.132 Blacks
more variable
Note that presuming that the disturbance variances in the two groups are equal results in a worsening of fit.
Equal Variances of Exogenous Variables
We force the two exogenous variances to be equal across Whites and Blacks.
Variable
Whites Blacks
Summary
SES
2.842
1.910 Whites more variable
Age
330.876
278.556 Whites more
variable
Note that presuming that the variances in the two groups are equal results in a worsening of fit. Also assuming that the groups have the same means and intercepts leads to falsely finding that Blacks are more variable on SES.
Exogenous Variables Correlation
Testing for the equality of the covariances makes little sense if the variances are not equal, but it is done so for illustrative purposes only.
Variables
Whites Blacks
Summary
SES-Age -12.727/-.45 -19.257/-.68 r more negative for Blacks
Despite the large difference between the correlations, the difference is not statistically significant.
Equal Error Variances
When we force the error variances to be equal, we find that the fit worsens quite a bit.
Variable Whites Blacks
Summary
X1 5.279
3.079 Whites more variable
X2
0.419 0.263
Y1
0.112 -0.102 Whites more variable
Y2
0.239 0.221
Y3
0.159
0.308 Blacks
more variable
Y4
0.104
0.221
Y5
0.124 0.199
We see that there is more error variance for the SES and Stress indicators for Whites, but there is more error variance for Black for the mental health factor. Note that there is Heywood case for Y1 for Blacks (negative error variance), likely caused by constraining Factor and Disturbance Variances to be equal.
Equal Factor Means and Intercepts
For the Neff data, we can test the equality of the means of the exogenous variables, Age and Stress, as well as the intercepts for the endogenous variables. For the endogenous variables, we have controlled for the two exogenous variables.
Variable Whites Blacks Summary
Age 46.310
43.320
Whites older
SES 5.953 3.369
Whites higher SES.
Stress 0.102 -0.706 Whites have more Stress
Mental Health 1.038 1.015 Blacks have slightly greater Mental Health
We note that imposing these constraints results in much worse fit, and thus there are race difference in the factor means and intercepts.
Summary of the Neff Example
Likely, the best fitting model is Model III, the model with equal loadings and paths. Perhaps we might wish to additionally allow for equal error variances.
![]()