David
A. Kenny
April 9, 2016
Miscellaneous Variables:
Formative Variables
and Second-Order Factors
Formative Construct
A formative construct or composite refers to an index
of a weighted sum of variables. In a formative construct, the indicators cause
the construct, whereas in a more conventional latent
variables, sometimes called reflective constructs, the indicators are
caused by the latent variable. Usually, a formative construct is defined as follows: There is a set of k exogenous variables (usually single-indicator measured variables) which
are combined to form an index. A latent variable C is created which has no
indicators or disturbance. One of the k paths leading into C is fixed to
one. Normally, all of the remaining paths are free, but they could be fixed.
The correlations or covariances between the k variables are free
parameters which are estimated. There is also one more endogenous variable which is called by C.
It need not be the case that causes or the formative variables are exogenous. Moreover, it is possible that the formative variable can have a disturbances, but additional constraints must be added to the model. For more discussion, see Bollen and Bauldry (2011, Psychological Methods).
An example of a formative construct is socioeconomic class or SES whose indicators might be Education, Income, and Occupational status. That construct causes Stress and Mental Health: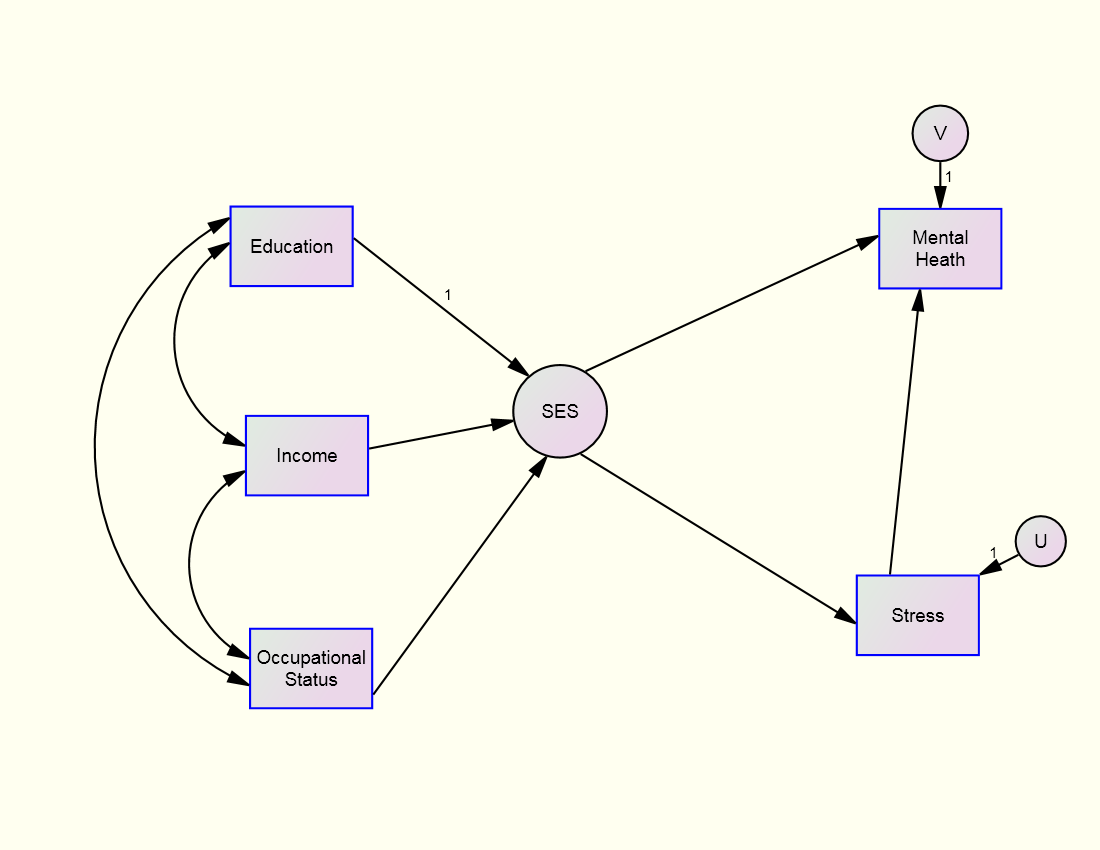
Note that the formative variable in the above model, SES, has no disturbance and the path from one of its indicators, Education, is fixed to one. The formative variable causes two endogenous variables, Stress and Mental Health. A key feature of a formative construct is that it mediates the effect of its three indicators on the endogenous variables of Stress and Mental Health.
Formative variables have many uses: First, if the researcher seeks to create a composite, a weighted sum of measured variables, a formative construct has optimal weights; second, if there is a nominal variable with many categories, the dummy variables for that variable can be the indicators of a formative variable (sometimes call a sheaf); third, if a reflective latent variable is planned, but either the indicators do not correlate or they are not single-factored, a formative variable might be used.
When
there is a single endogenous variable and no other exogenous variables, the standardized
paths leading into C are beta weights divided by the multiple correlation and the path from C to the endogenous variable is the multiple correlation. In
general, the standardized paths leading into C are proportional to canonical
coefficients.
To evaluate the utility of C to represent the paths from the k variables, drop
C from the model and have each variable cause the appropriate endogenous
variables. Compare the fit of this model to the one with C. The chi square
difference would have k(p - 1) degrees of freedom
where p is the number of endogenous variables. If fit is poor, then it means that the
composite should be formed different for the different endogenous variables.
Ken Bollen discusses in several papers how a formative construct can be endogenous and can have a disturbance, but those topics are not discussed here. If interested, go to his website.
Second-Order or Hierarchical Latent Variable
A second-order latent variable is a latent variable whose indicators are
themselves latent variables. Such a latent variable would then have no measured
indicators. It would have a disturbance if it were caused.
Rules of identification for latent variables still hold: The scale of the second-order factor must be fixed either by forcing one its loadings to one which is what is usually done or by standardizing the variable if it is exogenous and there must be a sufficient number of indicators, usually two are sufficient.
An example of a second-order factor might be Liberal-Conservative whose indicators might be the latent variables of attitude toward Social Issues, attitude the Economy, and attitudes toward Defense and the second-order latent variable causes desire to vote for two candidates, A and B:

Note that the second-order construct “mediates” the effect of the three first-order factors. Actually, it is not a mediator, but rather the second-order factor is a spurious cause of its indicators and the endogenous variables.
The major uses of a second-order are as follows: First, one has a construct but finds that it is multi-dimensional but by creating a second-order factor one can preserve the construct. Second, if a set of latent variables all cause the same construct, their colinearity may difficult to separate their effects, but by having the causality work through a single second-order factor, the colinearity is reduced. Third, by having just one latent variable instead of many, a second-order model is more parsimonious.
Note that first-order factors have disturbances which should not be viewed as measurement error. The disturbances reflect variance in the first-order factor not explained by the second order factor. The disturbance variance should be non-trivial and statistically significant. If not, then the first-order factor essentially correlates perfectly with second-order factor and and the two are no different. Heywood cases and negative disturbance variances are conceptually problematic. The researcher needs to check to be sure that they do not exist.
![]()