David
A. Kenny
September
11, 2011
Being revised after 12 years.
Please send
comments and suggestions.
Respecification of
Latent Variable Models
**These
simplifications in the model do not usually improve the model's fit and are in purple.
Those in black without asterisks may improve the fit of the
model.
Step A: Is the measurement
model consistent with the data (i.e., good fitting)?
Yes, go to Step C.
No, go to Step B unless you have exhausted reasonable respecifications.
IF SO, THEN STOP!
Step B: Revise the measurement model. (Go to the CFA page
for other ideas.)
Strategies
for respecification
correlation matrix
modification index (Lagrangian
multiplier in EQS)
definition: The approximate
increase in chi square if the parameter were free
zero implies parameter
already estimated
not identified
estimated as zero
sequence: a large modification
index may be explained by some other specification error
Some modification indices (especially with Amos) may be implausible and
should be ignored
standardized residual: Difference
between predicted and observed covariance standardized
What
to respecify?
Factor loadings
Too small?
Drop the measure?**
Too large, Heywood
cases?**
possible specification error
constrain error variance to be non-negative
Set the loadings equal? (Measures should have the same metric and the covariance matrix
analyzed.) **
Error variances
Too small or negative: Heywood cases?**
Set the error variances equal? (Measures should have the same metric and the covariance matrix
analyzed.) **
Need fewer factors?
Poor discriminant validity? (Combine factors.)**
Make sure each factor has sufficient variance. (Drop factors)**
Need more factors?
Run a maximum likelihood exploratory factor analysis to test the number
of factors (see how to do this). (Note that
this test presumes no correlated errors and so might be misleading if the true
model has correlated errors.)
Evaluate measures
Check to see if a
measure has large standardized residuals and modification indices (Lagrangian
multipliers in EQS). Consider dropping that measure.
Need correlated errors?
Considerations
Meaningfulness Rule: Only correlate errors for which there is a
theoretical rationale.
Transitivity Rule: If X1 is correlated with X2
and X2 with X3, then X1 should be correlated
with X3 unless one pair is correlated for one reason and the other
for a different reason.
Generality Rule: If there is a reason for correlating the errors
between one pair of errors, then all pairs for which that reason applies should
also be correlated.
Sometimes correlated errors imply an additional factor. For
example, if X1, X2 and X3 all have correlated
errors, then consideration might be given to adding a factor on which the three
load.
Single indicator
variables may not have correlated errors but indicators of other factors may
load on the single indicator "factor."
Which errors to
correlate?
large modification indices
large standardized residuals
Need measures to load
on more than one factor? (Read about
identification difficulties.)
When done return to
Step A.
Step C: If the structural
model is just-identified go directly to
Step D.
Are the deleted paths in the structural model
actually zero?
No, go to Step D.
Yes, add in deleted paths (see how deleted paths are defined) and go to Step D.
Step D: Are the specified paths of the structural model needed?
Yes, keep in model.
No, consider trimming from model.**
Equivalent
Models
Even if one's model fits, there are
a myriad of other models that fit as well.
These equivalent models should
be considered. Realize that for any model, there always exist an
infinite number of models that fit exactly the same. Thus, although the
fit of the structural model confirms it, it in no way proves it to be uniquely
valid.
Respecification Strategies
There are two strategies to take in
the process of re-specifying a model. One can test a priori,
theoretically meaningful complications and simplifications of the model.
Alternatively, one can use empirical tests (e.g., modification indices and
standardized residuals) to respecify the model. All respecifications
should be theoretically meaningful and ideally a
priori. Too many empirically based respecifications likely lead to
capitalization on chance and over-fitting (unnecessary parameters added to the
model). Ideally, if many respecifications are made, a replication of the
model should be undertaken. Although a priori hypotheses deserve the
initial focus, an examination of empirical tests of
miss-specification are in order. But if model changes are made on
the basis of such tests, there still need to be some sort of theoretical
rationale for them.
Example
Consider the following study:
Reisenzein, R. (1986). A structural equation analysis of Weiner's attribution-affect model
of helping behavior. Journal of Personality and Social
Psychology, 50, 1123-1133.
The study asks UCLA
students to imagine that they are on a subway and they see a man lying on the
ground and he appears to blind (a white cane is next to him) or drunk (an empty
whiskey bottle is next do him). Do you
help this man?
Measurement Model
Control Anger
C1:
controllable A1: anger
C2:
responsible A2: irritated
C3:
fault A3: aggravated
Sympathy Helping
S1:
sympathy H1: likelihood of helping
S2:
pity H2: certainty
S3:
concern H3: amount
Scenario:
single indicator dichotomy, no measurement
error, experimentally manipulated; 0 = blind and 1 = drunk
Structural Model
Control = Scenario + U1
Anger
= Control + U3
Sympathy = Control + U2
(disturbances of U2 and U3 correlated)
Helping
= Anger + Sympathy + U4
Specified Model
The fit of the
specified model is
χ²(60) = 87.507 p = .012 (fit: TLI =
.974 and RMSEA = .058)
Most investigators would stop
here. We adopt a different approach.
Note the df
of the measurement is 56 and the df of the structural model is 4, making the
total df 60.
Respecification of the Reisenzein
Model
Step A: Fit of the
Measurement Model or Just-identified Structural Model
χ²(56) =
81.63, p = .014 (TLI = .974; RMSEA = .058)
The fit is good, but it might be
improved.
Step B: Revised
Measurement Model
Let us examine at the largest
modification indices:
Covariances: M.I.
Par Change
E9 <-------------> Help 16.103 0.154
Regression
Weights: M.I. Par Change
S3 <------------- Help 10.581 0.198
S3 <---------------- H3 11.564 0.188
S3 <---------------- H1 11.500 0.187
The modification indices point to the S3 (concern) loading on the Help
factor.
Because this makes sense, the measurement model is revised allowing for
this loading. (One might argue that S3
should be dropped as it is not a clean indicator.)
Test Revised Measurement Model
χ²(55) = 58.89, p = .335 (TLI = .996;
RMSEA = .023 and 0 is in the 90% confidence interval)
There are no Heywood
cases and all of factor correlations (except between Scenario and Control) are
less than .85. The fit of the
measurement model is deemed acceptable.
We can live with this large correlation because it is in essence a
manipulation check.
Step C: Test of the
Deleted Paths (paths assumed to be zero)
The tests of the
deleted paths are as follows:
Cause Effect
Beta Z-Value
Scenario Anger .052 0.327
Scenario Sympathy .126 0.767
Scenario Helping -.354
-2.340
Control Helping
.186 0.836
So the only deleted
path needed is the path from Scenario to Helping. The path is negative indicating a willingness
to help the control person, the blind man, than the drunk
man. The combined test of the four
deleted paths is χ²(4) = 8.07, p < .10.
Step D: Test of the
Specified Paths and Correlation
All of the specified paths are statistically significant. However, the correlation between the disturbances of Anger and Sympathy is not statistically significant (Z = 1.213).
Step E: Trimmed Model
The correlation
between the disturbances of Anger and Sympathy is set to zero.
Factor Loadings
Factor
Variable Control
Sympathy Anger Helping
C1 .835
C2 .858
C3 .901
S1 .955
S2 .758
S3 .574 .349
A1 .885
A2 .822
A3 .841
H1
.941
H2
.923
H3 .786
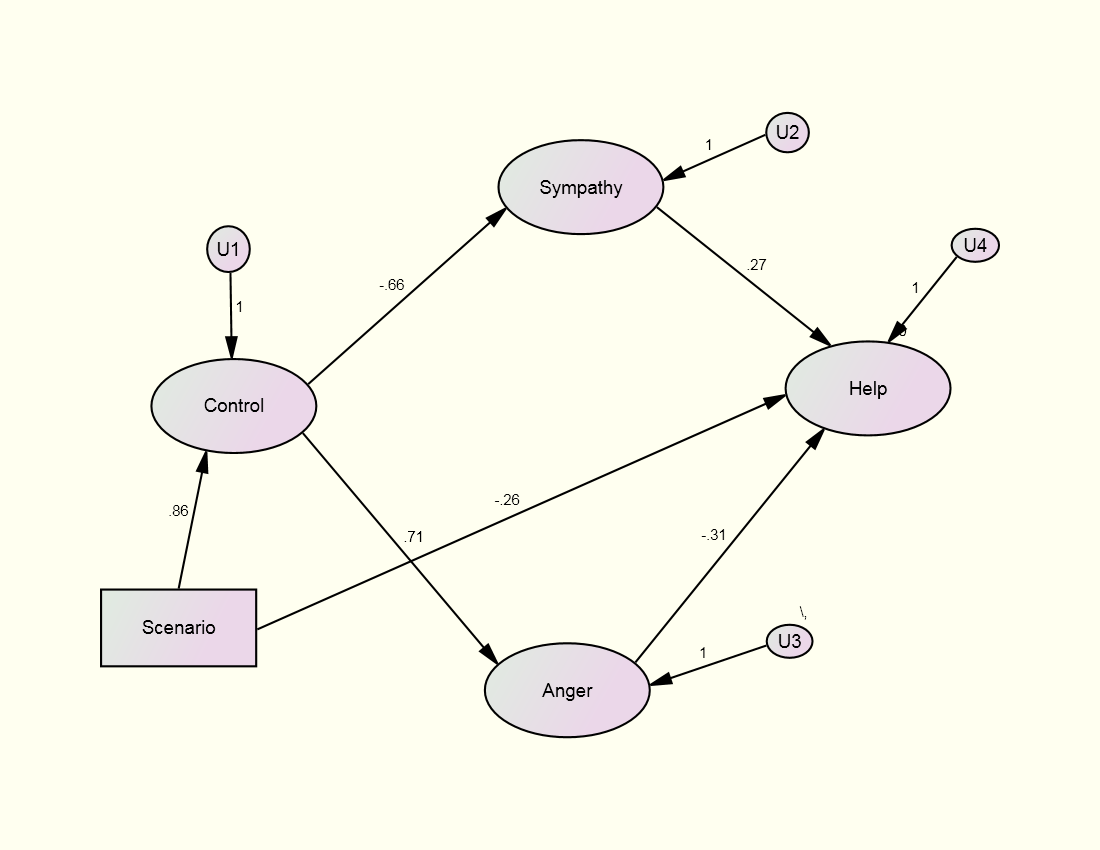
χ²(59) = 61.75, p = .378 (TLI = .997; RMSEA = .018)
R squared
Control .74 Sympathy .43 Anger .50 Help .50