David
A. Kenny
November 28, 1999
PRIMER
ON REGRESSION ARTIFACTS
Donald T. Campbell and David
A. Kenny
Forward by Charles Reichardt
The book is about
regression toward the mean: a person who is extreme on one variable
is unlikely to as extreme when measured on another variable. I started
this book with Donald
T. Campbell and completed it since Don's untimely death. Don considered
regression to the mean to be one of his most important contributions in
the field of methodology. The book considers the statistical, social,
biological, and political implications of regression to the mean. However,
most of the focus is on quasi-experimental evaluations of over-time data.
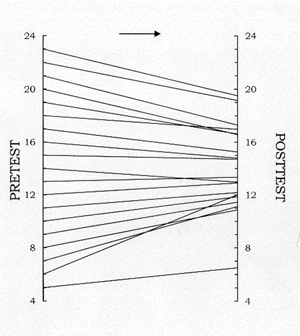 In the first chapter, we describe the phenomenon of regression toward the
mean in a non-technical fashion. We avoid presenting formulas but
instead focus on a graphical presentation. The emphasis is on the
conceptual and not the mathematical. The chapter presents the perfect
correlation line (see next paragraph), the pair-link diagram, and the Galton
squeeze diagram (illustrated in the paragraph), all of which are featured
throughout the primer. The Galton squeeze dramatically illustrates
the more extreme scores regress to the mean. The points on the left
are the scores on a pretest, and the points on the right are the posttest
means for the various scores on the pretest. A line connects the
two points. We see that larger scores at the pretest tend to become
smaller at the posttest, and smaller scores tend to become larger:
regression to the mean.
In the first chapter, we describe the phenomenon of regression toward the
mean in a non-technical fashion. We avoid presenting formulas but
instead focus on a graphical presentation. The emphasis is on the
conceptual and not the mathematical. The chapter presents the perfect
correlation line (see next paragraph), the pair-link diagram, and the Galton
squeeze diagram (illustrated in the paragraph), all of which are featured
throughout the primer. The Galton squeeze dramatically illustrates
the more extreme scores regress to the mean. The points on the left
are the scores on a pretest, and the points on the right are the posttest
means for the various scores on the pretest. A line connects the
two points. We see that larger scores at the pretest tend to become
smaller at the posttest, and smaller scores tend to become larger:
regression to the mean.
 This diagram is also featured in the primer. The jagged
line connected by circles is called the over-fitted line, a line
in which the means are connected to form a prediction line. The line
running through the over-fitted line is the regression line or least-squares
line. The flat line is the zero-correlation line (what the
regression line would be if there was no correlation) and the diagonal
is the perfect correlation line (what the regression line would
be if the correlation were one). Correlation can be thought of as
the relative distance of the regression line from the zero line.
The distance from the perfect correlation line to the regression line measure
the amount of regression to the mean. Regression to the mean can
be viewed as far the prediction (the regression line) is from perfection
(the perfect correlation line).
This diagram is also featured in the primer. The jagged
line connected by circles is called the over-fitted line, a line
in which the means are connected to form a prediction line. The line
running through the over-fitted line is the regression line or least-squares
line. The flat line is the zero-correlation line (what the
regression line would be if there was no correlation) and the diagonal
is the perfect correlation line (what the regression line would
be if the correlation were one). Correlation can be thought of as
the relative distance of the regression line from the zero line.
The distance from the perfect correlation line to the regression line measure
the amount of regression to the mean. Regression to the mean can
be viewed as far the prediction (the regression line) is from perfection
(the perfect correlation line).
In the second
chapter, we present the mathematics of regression toward the mean and answer
commonly asked questions about regression toward the mean or FAQs.
Among the questions considered are why regression to mean does not produce
mediocrity and how regression to the mean can occur when relationships
are nonlinear. We also generalize the concept beyond the simplifications
of the first chapter. Although this chapter is more mathematical
than the first, we still heavily rely on graphical methods.
The next six
chapters consider regression artifacts, the focus of the primer.
In Chapter 3, we show that when a group of persons are measured over time,
their average score regresses toward the mean. This chapter presents
several illustrations of regression to the mean in everyday life, including
the example that rookies of the year in baseball have a sophomore slump.
It also considers the often ignored problem of misclassification caused
by regression to the mean. It is suggested that perhaps as many as
40% of persons classified as "extreme" (e.g., gifted, disordered, or in
need of surgery) are not really extreme.
The next two
chapters consider regression to the mean in the nonequivalent control group
design. In this design a treated and control group are measured at two
time points. In Chapter 4, we show that matching of scores on a variable
only partially controls for group differences. Chapter 5 shows that
statistical equating ("partialling out" the pretest, like matching, is
not totally successful. We argue that statistical controls are usually
biased and the likely direction of bias can be determined.
Chapter 6 focuses
on the measurement of change and describes regression artifacts in change
score analysis. We learn that change is a much more difficult topic
than might be thought. We show that a person who does not change
at all may be the one who really "changed" the most once regression to
the mean is controlled!
The next two
chapters consider regression artifacts in more complicated situations.
Chapter 7 considers regression to the mean in time-series research.
We focus on the problem that the timing of the intervention often occurs
at an extreme point. Chapter 8 considers longitudinal research and
focuses on the idea of proximal autocorrelation. For both
of these topics we present several examples. In Chapter 9, we review
the once popular technique of cross-lagged panel correlation and urge its
revival. We show that it can be viewed as special type of multitrait-multimethod
matrix.
In the final
chapter, several themes are reiterated. These themes include the
utility of time-reversed analysis, graphical presentation of data, the
importance of design in research, and the consideration of plausible rival
hypotheses. We also discuss how forecasters and prognosticators often
fail to take into account regression toward the mean. We consider the case
of Sally and Sal. We see how Sal can be better forecaster than Sally
despite the fact that Sally's predictions are much more highly correlated
with the actual weather. The chapter also considers issues of epistemology
and the role of common sense in science.
Regression to
the mean can be very confusing and it has confused many (including Nobel
prize winners). A goal of the book is to take much of the mystery
out of this concept.
Download
the program that generated the figures on this page.
Go
back to the primer page.
 Go
back to homepage.
Go
back to homepage.
 In the first chapter, we describe the phenomenon of regression toward the
mean in a non-technical fashion. We avoid presenting formulas but
instead focus on a graphical presentation. The emphasis is on the
conceptual and not the mathematical. The chapter presents the perfect
correlation line (see next paragraph), the pair-link diagram, and the Galton
squeeze diagram (illustrated in the paragraph), all of which are featured
throughout the primer. The Galton squeeze dramatically illustrates
the more extreme scores regress to the mean. The points on the left
are the scores on a pretest, and the points on the right are the posttest
means for the various scores on the pretest. A line connects the
two points. We see that larger scores at the pretest tend to become
smaller at the posttest, and smaller scores tend to become larger:
regression to the mean.
In the first chapter, we describe the phenomenon of regression toward the
mean in a non-technical fashion. We avoid presenting formulas but
instead focus on a graphical presentation. The emphasis is on the
conceptual and not the mathematical. The chapter presents the perfect
correlation line (see next paragraph), the pair-link diagram, and the Galton
squeeze diagram (illustrated in the paragraph), all of which are featured
throughout the primer. The Galton squeeze dramatically illustrates
the more extreme scores regress to the mean. The points on the left
are the scores on a pretest, and the points on the right are the posttest
means for the various scores on the pretest. A line connects the
two points. We see that larger scores at the pretest tend to become
smaller at the posttest, and smaller scores tend to become larger:
regression to the mean.
 This diagram is also featured in the primer. The jagged
line connected by circles is called the over-fitted line, a line
in which the means are connected to form a prediction line. The line
running through the over-fitted line is the regression line or least-squares
line. The flat line is the zero-correlation line (what the
regression line would be if there was no correlation) and the diagonal
is the perfect correlation line (what the regression line would
be if the correlation were one). Correlation can be thought of as
the relative distance of the regression line from the zero line.
The distance from the perfect correlation line to the regression line measure
the amount of regression to the mean. Regression to the mean can
be viewed as far the prediction (the regression line) is from perfection
(the perfect correlation line).
This diagram is also featured in the primer. The jagged
line connected by circles is called the over-fitted line, a line
in which the means are connected to form a prediction line. The line
running through the over-fitted line is the regression line or least-squares
line. The flat line is the zero-correlation line (what the
regression line would be if there was no correlation) and the diagonal
is the perfect correlation line (what the regression line would
be if the correlation were one). Correlation can be thought of as
the relative distance of the regression line from the zero line.
The distance from the perfect correlation line to the regression line measure
the amount of regression to the mean. Regression to the mean can
be viewed as far the prediction (the regression line) is from perfection
(the perfect correlation line).